Creating a Learning Flow: A Hybrid Course Model for High-Failure-Rate Math Classes

Higher education in the United States is facing a failure-rate crisis in entry-level mathematics courses. In this article, we describe an innovative, technology-enhanced hybrid course model that has significantly improved course completion and content mastery outcomes in general education (GE) mathematics courses. The model relies on five primary components that are carefully articulated to create a reliable "flow of learning" for students. The approach has proven both cost effective and scalable to other courses and institutions.

Overview

Entry-level math classes at community colleges and state universities fill remedial and GE requirements and also serve as prerequisites for a range of higher-level courses in math and other subjects. Because of this, they are gateway courses for a vast range of majors — particularly those in high-demand science, technology, engineering, and mathematics (STEM) fields. Success in such courses is crucial; in fact, Clifford Adelman lists mathematics success as a key diagnostic for completing a STEM degree.¹

Students who arrive on campus requiring remediation or several semesters of lower-level math courses are unlikely to pursue or continue in a STEM major.² Historically, the completion rate for these courses has been low, and it has grown significantly worse in recent years. Influential reports published during the past eight years have presented evidence that the number of native-born U.S. graduates in natural science and engineering fields will fall far short of the trained professionals needed to replace the large number of projected retirees over the next 20 years.³ At California State University, Northridge (CSUN), data from the Office of Institutional Research indicates that between 50 and 60 percent of students receive grades below a C in GE mathematics courses. The numbers at other CSUs are comparable, and they are even worse at California community colleges (CCCs), hindering student transfers to four-year university programs. Particularly hard-hit are the "at-risk" undergraduates who predominate in most CSU and CCC student bodies. This group includes underrepresented minority and low-income students, most of whom are the first in their families to attend college. Failure to pass remedial and GE requirements negatively impacts retention rates and delays degree completion.

CSUN has developed an innovative, technology-enhanced hybrid course model that has both significantly improved student success and proven cost efficient and scalable. The model pairs a parent course (such as our course, Mathematical Methods for Business) with a one-unit supplemental hybrid course. Combined, the parent and hybrid courses provide five key components:

1. Online individualized remediation of prerequisite skills
2. Interactive lectures using materials shared across all course sections
3. Facilitated group work in a weekly supplemental contact hour
4. Online homework with instant feedback
5. Common student assessment tools shared across all course sections

In our implementations of the model at CSUN, the supplemental hybrid course has always included remediation (1) and facilitated group work (3), while the parent course includes components 2, 4, and 5. However, this breakdown is flexible and can be adapted to the physical, personnel, and financial resources available. The instruction is divided among faculty, who teach the parent course, and graduate teaching assistants (TAs) and undergraduate tutors for group work and remediation. Together, they coordinate weekly content and instructional approaches to create a "flow of learning" for the student. This flow moves students actively and successfully from classroom work, to group work, to homework, to exams.

The model components incorporate interventions and practices — such as support for mathematics success, problem-solving in teams, and interaction with instructors beyond the lecture setting — that have proven successful at CSUN and other campuses in supporting students, particularly those from underrepresented minority and disadvantaged economic groups.⁴ The model's structure and the interdependence of its five components are described in a web-based interactive video presentation (see Figure 1). The presentation integrates pictures, text descriptions, interviews with instructional staff and students, video footage of learning activities, and links to support resources into a single package. This presentation has been used to orient and train instructional staff wanting to adopt the model.

Figure 1. Web-Based Interactive Video Presentation

CSUN Implementation and Results

In 2008, this course model was implemented at CSUN in the gateway Math 103 (Mathematical Methods for Business) course. The results have been dramatic, essentially reversing the downward trend in student success:

• Prior to implementation, less than 34 percent of students received a final grade of C or better.
• Post-implementation, more than 66 percent of students achieve a C or better in Math 103.

These results have been sustained over seven semesters. Figure 2 compares the histograms of the grades on the final given in the semester before implementing the model in fall 2007 (blue) and the one after in spring 2008 (green). Note that the final each term is common to all sections of Math 103 and is collaboratively graded by the instructors and TAs. The exam varies somewhat from term to term, but not so significantly that comparisons cannot be made. The x-axis shows different percent ranges on the final exam, while the y-axis shows the percent of students in that range. For example, the height of a bar over 75 shows the percentage of students in each term that achieved 75–80 percent on the final. As the graph shows, there was a vast improvement in both the students' average scores and the distribution of the grades.

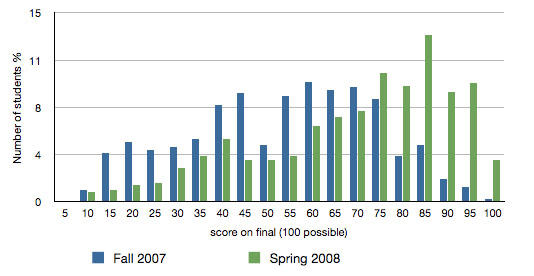
Figure 2. Final Exam Results Before and After Model Implementation

This cost-effective model offers a significant return on investment. The cost savings in reducing the number of students repeating the course (approximately $20,000) more than compensates for the additional instructional costs for enrolling students in the one-unit supplemental hybrid course (approximately $16,500). For example, in Math 103 at CSUN, typical enrollment is 600 students, with approximately 500 enrolled in the hybrid lab (Math 103L). These 500 Math 103L students are taught by graduate TAs, who teach six units per term and are paid $6,648. The students are broken into 10 sections at an instructional cost of $16,620. To calculate the savings, we know that the C or better rate in Math 103 rose from one-third to two-thirds after implementing the hybrid lab model. Thus, for each term, approximately 200 students who would have previously repeated the three-unit class are no longer doing so. This translates into three to four fewer Math 103 sections, at a savings of at least $20,000. Thus, the net savings exceeds $3,000 per term. This money is used to provide additional tutoring both in the contact hour of Math 103L and in the tutoring centers.

To implement this model, the only significant initial investment was providing course release or additional pay to faculty to develop the course and lab materials. At CSUN, we set up the program in four classes with modest grants from the university's Department of Mathematics, as well as funds from the CSU system and (more recently) from the Next Generation Learning Challenges (NGLC). This funding totaled approximately $60,000.

The hybrid labs do not require any special facilities. We use standard classrooms for the contact hours and standard computer labs to support the lab's online component. At CSUN, no additional facilities have been constructed for this purpose; indeed, facilities previously lying empty in the afternoon and evening Monday through Thursday and all day on Fridays are now buzzing with activity (Figure 3). Because the remediation component is web-based, students can either come to the computer labs, where they get help from peers and tutors, or access it when it best suits their schedules and readiness for learning. They are required to come into the computer lab only once for a proctored final assessment on the prerequisite skills.

Figure 3. Students in the Computer Lab at CSUN

Because of its success, use of this model has now expanded to all lower division pre-calculus and calculus courses at CSUN. It has also been implemented successfully at California State University, Long Beach (CSULB), and is being expanded to other courses there. Also, in 2012–2013, Pierce College in Los Angeles and Humbolt State University in Northern California will both implement the model, with funding from an NGLC Wave I grant.

Theory of Change Underlying the Model

The hybrid course model seeks to overcome three obstacles to learning:

• Weak student prerequisite knowledge upon course entry
• Passivity in the students' instructional experience
• Inconsistent and poor-quality instructional practice in large multisection classes

Our interactive video presentation describes how these three problems are directly addressed through the five model components:

1. Individualized remediation
2. Interactive lectures
3. Facilitated group work in a supplemental contact hour
4. Online homework with instant feedback
5. Common student assessment tools

As Figure 4 shows, the structure and relationship of the five components facilitates the "learning flow" that moves students actively and successfully from classroom work, to group work, to homework, to exams.

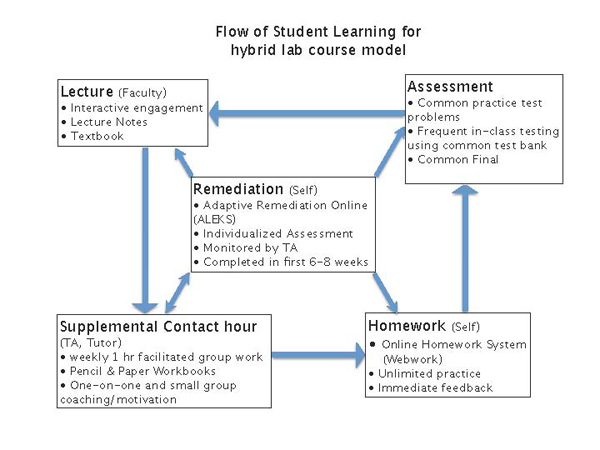
Figure 4. How Students Flow through Math 103/103L

Once in place, the flow created by the five components and the instructional staff's coordinated efforts gradually moves the student from passive listener to independent learner. In the hybrid model, students constantly refresh remedial knowledge/skills so as to:

• Arrive at the lecture ready to see a new concept
• Arrive at the supplemental contact hour ready to practice that concept in facilitated group work
• Approach their homework ready to work independently
• Return to the lecture ready for an expansion on that concept, the introduction of a new concept, or an assessment of retention

This flow addresses the first two learning obstacles: weak prerequisite knowledge and passivity in learning.

The learning flow is made clear to students through their interactions with instructors and coordination of the lecture notes, supplemental contact hour workbook, and homework. When they leave the classroom or group-work session, they know precisely what their next steps are and how those steps correlate to the previous one. The faculty, graduate assistants, and tutors are trained to be aware of all the course materials and coordinate their efforts so that lecture topics are followed up on in lab, homework, and exams. Achieving this level of clarity supports the instructional staff and addresses the third obstacle above: consistency of instructional practice across multiple sections of the same course.

In discussing the model's five components, we begin with remediation, as it is essential to success in all four of the other components. It is also the least familiar and most innovative part of the hybrid course model and thus takes some time to explain. Following that, we discuss the other four components together, as their success is tied to the coordination of their activities — with the key point being to find or create closely correlated material for the lectures, supplemental contact hours, homework, and exams.

Component 1: Remediation

A student's facility with prerequisites is particularly important in mathematics courses, where the scaffolding of knowledge and skills plays a fundamental role. For example, students cannot build and interpret an equation that models business profits if they have trouble using algebra and arithmetic to create and manipulate the model. Traditionally, the list of courses on a student's transcript is used as the only measure of preparedness. However, the crisis in passage rates across the United States indicates that this is a poor predictor of student readiness. In particular, it does not account for when the prerequisite course was taken or whether its emphasis or depth matches the current course's needs.

In the hybrid course model, all students attend the parent course lectures, do the online homework, and take the common assessments (tests), while the remediation and supplemental contact hour are reserved for those students whose weak prerequisite knowledge indicates that extra help is necessary (see Figure 5). Placement in the lab is determined by proctored online prerequisite testing that feeds directly into the registration system. In this way, we ensure that after the first few weeks, students have the prerequisites for each new concept at their fingertips.

Figure 5. Placement into Math 103/103L

Technology allows us to cost-effectively tailor a student's remediation to his or her mathematical and educational background. This ensures that each student is productively struggling rather than floundering. We use an online, self-paced course focused on the prerequisite knowledge required to succeed in the parent course. In most implementations, we use ALEKS (Assessment and Learning in Knowledge Spaces), a commercial intelligent tutor software system (see Figure 6).

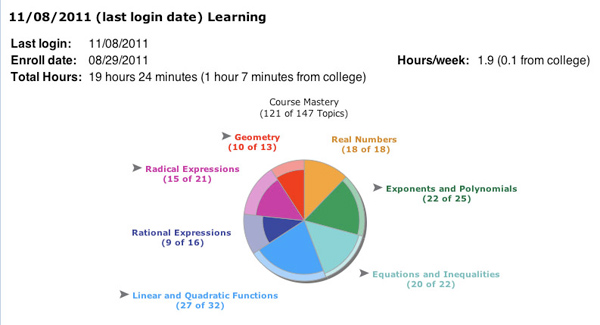
Figure 6. The ALEKS Intelligent Tutor Software System

The ALEKS program dynamically tests students to assess their area of competence and then dynamically directs them along an individualized instructional pathway. The program uses artificial intelligence software developed by the University of California, Irvine, and the US National Science Foundation to continually adjust to a student's state of knowledge and what he or she is most ready to learn next. This assessment information is displayed as a pie chart that students can click on to get their next topic of study. In this way, students work on only their personal areas of weakness, and their progress is broken down into intermediate objectives that must be achieved each week.

ALEKS is a continuously updated service that students access for a fee of $30 for six weeks. TAs monitor the service; a single TA can successfully monitor and motivate the progress of approximately 160–200 students. This is because the same TA meets these students weekly in the supplemental contact hour in groups of 40–50. At that time, the TA encourages, cajoles, and convinces students to stay on track with their ALEKS remediation. CSUN and CSULB have found that this face-to-face time is essential to the success of the program's remediation component.

Components 2–5: Inspiring Participation and Coordinating Content

The next four components of the hybrid course model address student passivity and the need for consistency across multiple sections. In our experience, the passivity problem is strongly rooted in a misconception among students and instructors — namely, that recognition equals learning. Watching an instructor work a problem and recognizing that the steps seem correct is passive and not predictive of the student's ability to complete the same or similar task independently.⁵ Learning requires the student's active participation, moving from listening, to practicing, to explaining, and finally to performing on exams. In both the lecture and the supplemental contact hour, the goal is to have students working and thinking as much as possible. By carefully coordinating course materials for these two components, a flow is created from class lecture work to group work. By further coordinating these materials in the homework and assessment tools (exams), this flow continues in the student's individual performance. The homework can include interactive reading of online lecture notes and readings. The focus is on coordinating the content of these materials, rather than perfecting any one element. The Supplemental Materials section of our video presentation offers examples of the course materials.

As a case study of what it means to "coordinate" the content of course materials, consider CSUN's Business Math course, Math 103. One overarching goal is that students can read a problem in the business context, know which mathematics model the problem, solve the problem mathematically, and then summarize their solution in a sentence in the business context. It turns out that this is extraordinarily hard for students to do. Thus, they need to see this skill demonstrated in lecture, practiced in group work during the supplemental contact hour, and mastered in homework. Only then can we expect students to demonstrate the skill on exams.

For example, a capstone topic in Math 103 is Elasticity of Demand. A typical question asks:

A company manufactures and sells x widgets per week with a price demand function p(x) = 40 − .1x

1. Solve p = 40 − .1x for x in terms of p to get a function f(p) which gives the demand at a price p.
2. Compute the elasticity of demand function for this price-demand function.
3. At p = $8 per widget a price increase of 4 percent will create what change in demand? Write a summary statement.
4. At a price of $8 per widget are revenues increasing, decreasing, or remaining constant? Why? Write a summary statement.

Parts (a) and (b) are fairly computational. However, they lead to parts (c) and (d), which require the student to return to the business context. A correct summary statement for (c) could be: "At a price of $8 per widget, a price increase of 4 percent will create a demand decrease of 1 percent."

The threshold for a correct response to (c) is that the units are correct and a layman could understand the answer without additional context. A correct answer for (d) could be: "At a price of $8 per widget, revenue is increasing because demand is inelastic, meaning that a small percent increase in price results in an even smaller percent decrease in demand." The threshold for part (d) is that a peer in the class could understand the statement without additional context.

The format and wording of the problem might vary between problems. For example, as students become more practiced, part (a) can be shortened to: "Find a function f(p), which gives the demand at a price p." What is essential, however, is that as students move from lecture, to supplemental contact hour, to homework, and then to testing, they are consistently able to read a contextual problem, know what math to implement, implement it accurately, and put their answer back into context. Although this coordination seems obvious, in our experience this is where student learning most commonly breaks down; while experts see the connection between these concepts/skills in lecture, homework, and testing as clear, students see it as murky.

Implementation Issues

Coordinating diverse course materials, as well as remediation efforts, in a way that consistently communicates expectations starts with the thoughtful development of materials. However, as we now describe, it also requires careful choice of technology, intense training of instructional staff, and an assessment cycle of the materials and teaching practices.

Software and Materials

At CSUN, we use a mix of open-source and commercial software as well as old-fashioned pen-and-paper work, depending on our objectives. For remediation, we use the ALEKS intelligent tutor; for homework, we primarily use Webwork, a free, open-source online homework system for math and sciences courses. Although Webwork does not adjust its content to student performance, it does serve as a mechanism to get homework to the students and to give them unlimited practice and instant feedback on their work. For the supplemental contact hour, we use pen-and-paper workbooks purchased by the students; here, the focus is on the act of writing mathematics as a connection between lecture, homework, and exams. These elements are coordinated with the work of the faculty and TAs, as well as with other course materials: lecture notes, supplemental contact hour workbooks, homework problems, and exam problems.

Training for Instructional Staff

One challenge we have observed in the existing implementations of the hybrid model has been training instructional staff in how the model works and when, where, why, and how to use its accompanying resources. Because of the model's complex structure and heavy interdependence of the components, pre-term meetings and training are essential, and midterm training is being considered. Instructors of the parent lecture courses must know how the remediation and supplemental contact hour support the material presented in class and must focus on the agreed-upon student learning outcomes. In particular, these instructors must know and follow the schedule and points of emphasis for each topic. Thus, they must understand the model and be familiar with the resources for all of its components.

Instructors in the supplemental contact hour and those monitoring the remediation must be familiar with all of these resources as well. They must coordinate with the parent class so that students see early on that their time on task in these additional activities has a direct impact on their success in the parent course. This creates buy-in among the students and is fundamental to the model's success.

CSUN and CSULB have started developing hybrid training programs that provide some aspects of training online. This includes our interactive video presentation, online access to all course materials and common syllabi, and mandatory online quizzes on those materials. This is managed through Moodle, an open-source academic learning management system. By providing some training online, we can streamline the start of term meetings and focus on the "big picture" of how the hybrid course model's five components fit together.

Assessment Cycle

Another aspect of our hybrid model is the assessment cycle for continually improving the model's implementation. In the case of CSUN's Math 103, the course structure has stabilized, but the materials are constantly revised. These materials include common lecture notes, workbooks for the supplemental contact hour, online homework, and a final given and graded in common. Each term, all 500–600 Math 103 students have their individual scores recorded for each of the 10 multipart problems on the common final. This allows for careful item analysis and discussion of student learning objectives at the end of each semester. That analysis directs modifications during the semester breaks for immediate implementation in the subsequent term. Additionally, grades can be sorted by instructor for individual faculty development and improvement. Over a longer period, passage rates and success in subsequent courses are used to measure the course's effectiveness and to suggest modifications to the model. This assessment cycle is fundamental to our technology-enhanced hybrid course model.

Evidence Supporting the Hybrid Model

To measure the model's success, we looked at three measures of student success:

• Content mastery
• Student learning outcomes (SLOs)
• Deeper learning outcomes (DLOs)

We looked at data from the term just before and the term just after implementation of the hybrid course model, as well as longitudinally over 10 terms (three pre-implementation and seven post-implementation). Content mastery was measured using course grades (collected by CSUN's registrar) and common final exam scores (collected by the course coordinator). The course grade data was provided by the university's Institutional Research departments.

We use both the letter grade in the course and the final exam score to measure content mastery. We say that students have mastered a class based on their letter grade if they receive a C or better in the course. We say that they have exceeded expectations based on their letter grade if they receive a B or better in the course. We say that students have mastered a class if they receive a score of 70 percent or better on the final exam. We say that they have exceeded expectations if they receive 83 percent or better on the final exam. In all implementations so far, the final exam is common to all sections and is graded collaboratively by the instructors and TAs just after it is administered to the students. The scores are recorded problem by problem for each student just after grading and collected by the course coordinator on that day. Make-up exam scores for students who missed the final are not counted in the data. We measure SLOs based on student performance on the corresponding problems on the common final exam, and DLOs by student performance on the most cumulative and/or challenging final exam problems. We say that a student has mastered an SLO or a DLO if they receive 70 percent or better on the corresponding problem or problems.

Some history helps put this data in context. This course model started at CSUN in the Business Math course. Prior to fall 2006, business majors took a generic college algebra class (Math 102) as their Business Math GE requirement. In fall 2006, CSUN created Math 103, which covers the college algebra and calculus needed for business applications. We ran Math 103, as an experimental topics course, which author Katherine Stevenson taught in two sections to 65 students. In spring 2007, this new course became the requirement for all business students but was taught without the supplemental contact hour and remediation components. In spring 2008, these components were implemented. In fall 2008, Math 103 with the full hybrid course structure was adapted to CSULB's Business Math course, Math 115.

Results Before and After the Hybrid Lab Model Implementation

The results achieved through completed implementations of this hybrid model are remarkable. At CSUN, the average score for 12 sections of Math 103 in spring 2008 on the common final was 70 percent — an improvement of more than 20 points over fall 2007. Thus, the average spring 2008 student was at or close to content mastery as measured by the final. Also, we saw greatly improved homogeneity across sections of Math 103: In fall 2007, the section-to-section averages on the common final ranged from 23 to 70 percent; in spring 2008, they ranged from 60 to 81 percent. Moreover, for students in the two large sections (100–120 students each), the mean final exam scores were 67 and 70 percent, respectively, up from 53 percent in fall 2007. This is on par with students in the smaller sections, showing that our model is cost-effective without sacrificing student learning.

There was also a marked performance improvement in SLOs in all but one category between fall 2007 and spring 2008. Figure 7 compares the median scores on SLO-related problems from the common final in fall 2007 and spring 2008. The topics above the diagonal dotted line indicate improved performance. The derivative problem demonstrated no improvement, but this is not surprising, as the supplemental contact hour and remediation focus more on the course's capstone topic — maximizing profit — and the major problem areas of graphing, piecewise functions, elasticity, and solving systems of equations. Modeling Cost showed a small decline in student achievement, but because it was already high, this was not a concern.

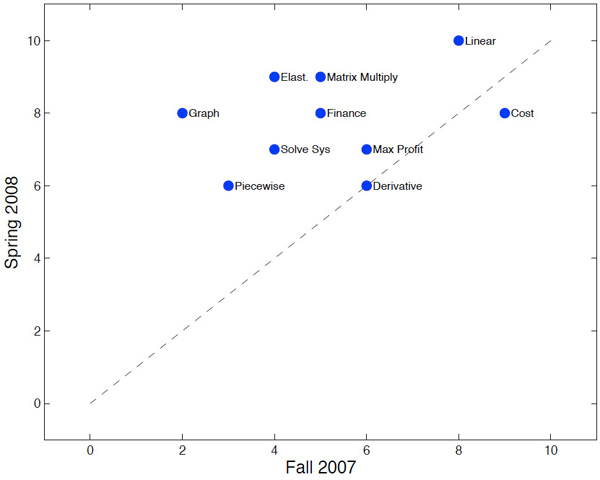
Figure 7. Median Scores on SLO-Related Final Exam Problems

NGLC defines DLOs as student success on cumulative and/or challenging concepts. We measured this by looking at student performance on the three problems that the Business School identified as fundamental and overarching goals for the course:

• Maximize profit via calculation: use calculus and algebra to compute marginal revenue and marginal cost and use these to maximize profit in a business situation problem.
• Maximize profit via graphical interpretation: in a business situation, graph revenue and cost, use the graph to maximize profit, and interpret how change as fixed and variable costs change profits.
• Elasticity: compute and interpret sensitivity of demand to price changes.

Here, as with SLOs, we see marked improvement in the results from fall 2007 to spring 2008. As Figure 8 shows, the shape of the distribution of student scores is greatly improved. Moreover, in spring 2007, only 40 percent of students achieved DLO mastery (scoring at least 21 points out of 30 possible, for 70 percent or better), while in spring 2008, 58 percent of students achieved DLO mastery.

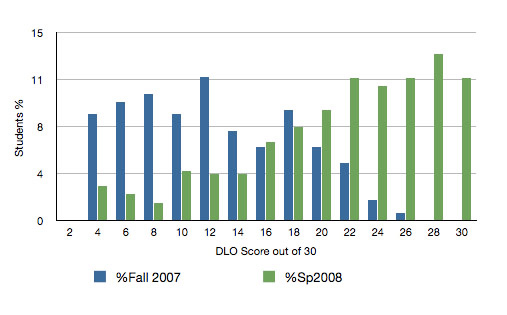
Figure 8. DLO Mastery on Math 103 Final Exam Before and After the Hybrid Lab Implementation

Longitudinal Results Before and After the Hybrid Lab Model Implementation

The improved results in content mastery, SLOs, and DLOs in spring 2008 have been sustained over the seven semesters since the hybrid labs were implemented. Figure 9, provided by CSUN's office of Institutional Research, plots student final grades that exceeded or failed to meet content mastery standards term-by-term over 10 semesters (As and Bs are in blue; Ds, Fs, and Us, or unauthorized withdrawals, are in red).

Figure 9. Semester Student Grades and Content Mastery for Math 103 (%)

As described earlier, in fall 2006, 65 students participated in a prototype course; in spring and fall 2007, Math 103 without hybrid labs was required for all business students; and in spring 2008, the labs were implemented. As Figure 9 shows, a stable and healthy percentage of students exceeded expectations over time (blue). This is a marked improvement over the period before the labs were implemented, as well as significantly better than student performance during the same period in Math 102, the class that Math 103 replaced (see Figure 10).

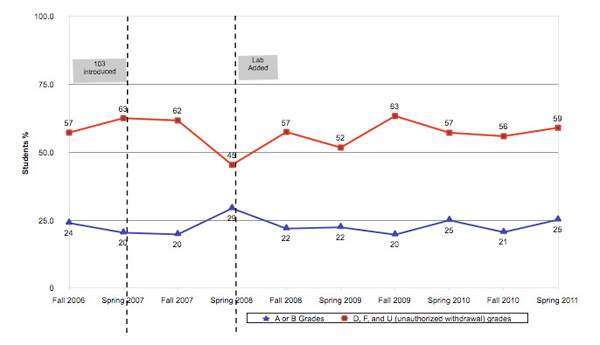
Figure 10. Semester Student Grades and Content Mastery for Math 102 (%)

As with content mastery, the DLO results have remained consistently strong since spring 2008. Table 1 shows the percentage of students achieving 70 percent or better on the DLO exercises in each of the nine reporting terms. Interestingly, while content mastery improved from spring 2007 to fall 2007, DLO mastery fell substantially in that period, from 40.26 percent to 6.86 percent. Even factoring in for variations in problem difficulty on a given topic from one term to the next, this seems a poor result. However, this period was prior to the course redesign. In the post-redesign model, with the labs in place, there was a sustained improvement in DLO results.

Table 1. Students Scoring 70 Percent or Better on DLO Exercises

At CSULB, data collected for the Business Math Course (Math 115) demonstrates that student success is correlated to completion of remediation and success in online homework. For example, in the Math 115 sections studied, students who had a homework average of 70 percent had a .9 probability of passing the class, whereas those with a homework average below 50 percent had only a .44 probability of passing. To look at remediation's effect on student success, we considered two remediation milestones: more than 64 percent of remediation topics completed by week 4, and more than 84 percent completed by week 6. Students who completed 85 percent of the topics by week 6 had a .86 probability of passing the course, whereas students who completed at least 65 percent by week 4, but did not complete the 85 percent by week 6, had a .69 probability of passing the course.

Finally, as the evidence culled from implementing the model shows, online remediation and homework alone are not enough to turn around a high-failure-rate class. In fall 2007, CSUN tried implementing the online remediation and online homework without the group-work labs, and in spring 2007, we tried supplemental instruction without online remediation. Although there were minor improvements in the passage rates, we saw no significant improvement in common final scores. The combination of group-work labs and remediation is fundamental to making substantial improvements in high-failure-rate GE math courses. Moreover, the combination is essential to improving outcomes tied to deeper learning. Technology can help us tailor the student's experience, but we believe that, ultimately, we are social animals and students need someone "advocating" for the time spent remediating and working on course content.

Conclusion

The hybrid course model has proven effective at CSUN in turning around high-failure-rate math classes. It increases student success and their deeper learning. Moreover, it does so in a cost-effective, scalable way. It has also been successfully applied to other classes and at other institutions. Unlike many other models, such as modularization or emporium-style learning, our model does not require large-scale facility redesign, and it leaves the parent course as a standard free-standing course under an instructor's control.

The model does require well-coordinated course materials, access to technology, and a teaching staff willing to coordinate their work in order to improve student performance and ultimately lessen the faculty's burden. The model's five key components and the course/hybrid-lab structure foster the desired environment, which helps instructors and students better allocate their time and better choose what to do in that time. Students learn how to break down their learning into steps and follow those with consistency. They enter the class as passive listeners and leave as active, independent learners. In this environment the flow of learning is clearer to the student and its rewards are immediate and consistent, with proven results.

Acknowledgments

We gratefully acknowledge the work of the various instructors, TAs, tutors, and staff who have contributed to this project. In particular, we thank CSUN's Professor William Watkins for his work on the Math 103 course materials and CSULB's Professor Florence Newberger for her implementation of the model at CSULB. In addition, we acknowledge Joel Bennett for his extensive work on the interactive video presentation included in this article. Finally, we thank the reviewers, and the editor, for their helpful comments and suggestions.

1. Clifford Adelman, Answers in the Tool Box: Academic Intensity, Attendance Patterns, and Bachelor's Degree Attainment (Washington, DC: U.S. Department of Education, 1999), and The Toolbox Revisited: Paths to Degree Completion from High School through College (Washington, DC: U.S. Department of Education, 2006).
2. Suzanne G. Brainard and Linda Carlin, "A Six-Year Longitudinal Study of Undergraduate Women in Engineering and Science," Proceedings of Frontiers in Education, vol. 1, 1998, pp. 134–143; Adelman, Answers in the Tool Box; and T. Carter Gilmer, "An Understanding of the Improved Grades, Retention, and Graduation Rates of STEM Majors at the Academic Investment in Math and Science (AIMS) Program of Bowling Green State University," Journal of STEM Education, vol. 8, no. 1, 2007, pp. 11–21.
3. National Academy of Sciences, National Academy of Engineering, and Institute of Medicine, Rising Above the Gathering Storm: Energizing and Employing America for a Brighter Economic Future (Washington, DC: National Academies Press, 2007); and National Science Board, The Science and Engineering Workforce: Realizing America's Potential (Washington, DC: National Science Foundation, 2003).
4. Simeon P. Slovacek, Susan Tucker, and Jonathan C. Whittinghill, "Modeling Minority Opportunity Programs: Key Interventions and Success Indicators," Journal of Education and Human Development, vol. 2, no. 1, 2008; Maria Teresa V. Taningco, Ann Bessie Mathew, and Harry P. Pachon, STEM Professions: Opportunities and Challenges for Latinos in Science, Technology, Engineering, and Mathematics (Los Angeles: Tomás Rivera Policy Institute, 2008); Adelman, Answers in the Tool Box and The Toolbox Revisited.
5. John Dewey, How We Think: A Restatement of the Relation of Reflective Thinking to the Educative Process (Lexington, Massachusetts: D.C. Heath & Co., 1933); and Elena Marchisotto and John Hartzog, "Mathematics 095, Review of Pre-College Mathematics: A Modular, Multi-Media Course," International Journal of Mathematical Education in Science and Technology, Vol. 15, No. 2, 1984, pp. 221–230. Marchisotto formerly was the CSUN developmental math director.

© 2011 Katherine Stevenson and Louis Zweier. The text of this EQ article is licensed under the Creative Commons Attribution-Noncommercial-Share Alike 3.0 license.